Reading notes: Risk-Adjusted valuation of R&D projects

In this article Boer describes R&D management as the art of creating value by managing an extraordinary degree of risk. He proposes a unified approach to valuating R&D projects combining Net Present Value (NPV), Discounted Cash Flow (DCF), Decision Tree (DT) and Real Options (RO).

Payoffs from the R&D projects are diminished by what Boer calls Three Horsemen of the R&D Apocalypse:

1. the time value of money,
2. the risk of technical failure, and
3. the cost of the R&D program itself.

Unified approach to the valuation of an R&D project

Boer's unified approach to the valuation of an R&D project consists of three analytical tools:

• Discounted Cash Flow,
• Decision Trees, and
• Real Options.

He explains that DCF is known to systematically underestimate the value of R&D projects (and other intangible assets), DT quantifies unique risk and creates value by structuring R&D programs into a series of go/no-go decision points that exploit the option to abandon, and how RO is more appropriate for valuation of R&D project plans than Discounted Cash Flow because plans are options, not assets. (Boer, 2003, pp. 50–51)

In effect this unified valuation results in a a compound option based on multiple options to abandon, which also incorporate the value of call options capturing market risk. (Boer, 2003, p. 51) It is performed in two steps:

1. Use Discounted Cash Flow to obtain a best estimate of business plan value.
2. Use Decision Tree with Real Options to capture full value of both unique and market risk, as well as option to abandon.

This approach to valuation is fit for situations with high risk, exposure to volatile markets, longer time horizons, and progressively increasing development costs. Some examples Boer mentions are industrial R&D, venture capital, petroleum exploration and screen-play development. He points that the biggest benefit might come from investing into opportunities that competition will pass over because they haven't seen the value of it.

Setting up the calculation

1. Framing the problem.

Understand the business situation and frame the option credibly, leverage own and experts knowledge, identify and analyse the assumptions that are driving the variance between numbers and expert opinion.

2. External/financial inputs.

There are three financial inputs required:

• Risk-free Interest Rate. Usually considered to be the return on Treasury bills. Boer uses 5% in his example.
• Cost of Capital for the party funding the project. Boer uses 12% in his example.
• Volatility. Expressed as the annual standard deviation of the value of the security underlying the option. For a real option, the underlying security is the present value of the business plan. Present value can be calculated by adding together Initial Investment and Net Present Value.

Boer proposes following ways of estimating volatility by using:

• the observed volatility of stocks in the industrial sector in which the business plan operates,
• the observed volatility of the parent company,
• the volatility of a time series of prices in a commodity to which the business plan is linked (such as natural gas), and
• the volatility of the cash margin of the product to which the business plan is linked.

Once volatility has been estimated, Boer recommends us to run a simple sensitivity analysis by running a base case, favourable case, and conservative case.

3. Business inputs

Two business inputs taken from the business plan are:

• the Net Present Value, and
• the Initial Investment.

Boer recommends to use sensitivity analysis or Monte Carlo simulation to determine the range of uncertainty in Net Present Value. Pre-commercial R&D costs should not be front-loaded, as that presents the project as an all-or-nothing case, and we lose the the benefits of the option to abandon.

4. R&D inputs

Each R&D stage requires following three inputs:

• estimated duration of the stage,
• estimated after-tax cost of the stage, which is actual cost $\times$ (1 - tax rate), and
• the probability of success defined as the probability of advancing through the stage gate to the next stage.

In Boer's example four stages are Conceptual, Feasibility, Development, and Early Commercialization / Launch. Research managers are important for estimating stage duration and cost, while estimating success should be done on the basis of expert opinion and reviewing statistics. On the latter, Boer recommends creating a database of projects and tracking what percentage of candidates  advances to each next stage.

Example of unified approach to valuation of R&D projects

The fictional example focuses on developing a new microorganism. There are two R&D stages over three years. First one is a one year feasibility study, and second is two-year field test.

Project outcomes by DCF/Decision Tree

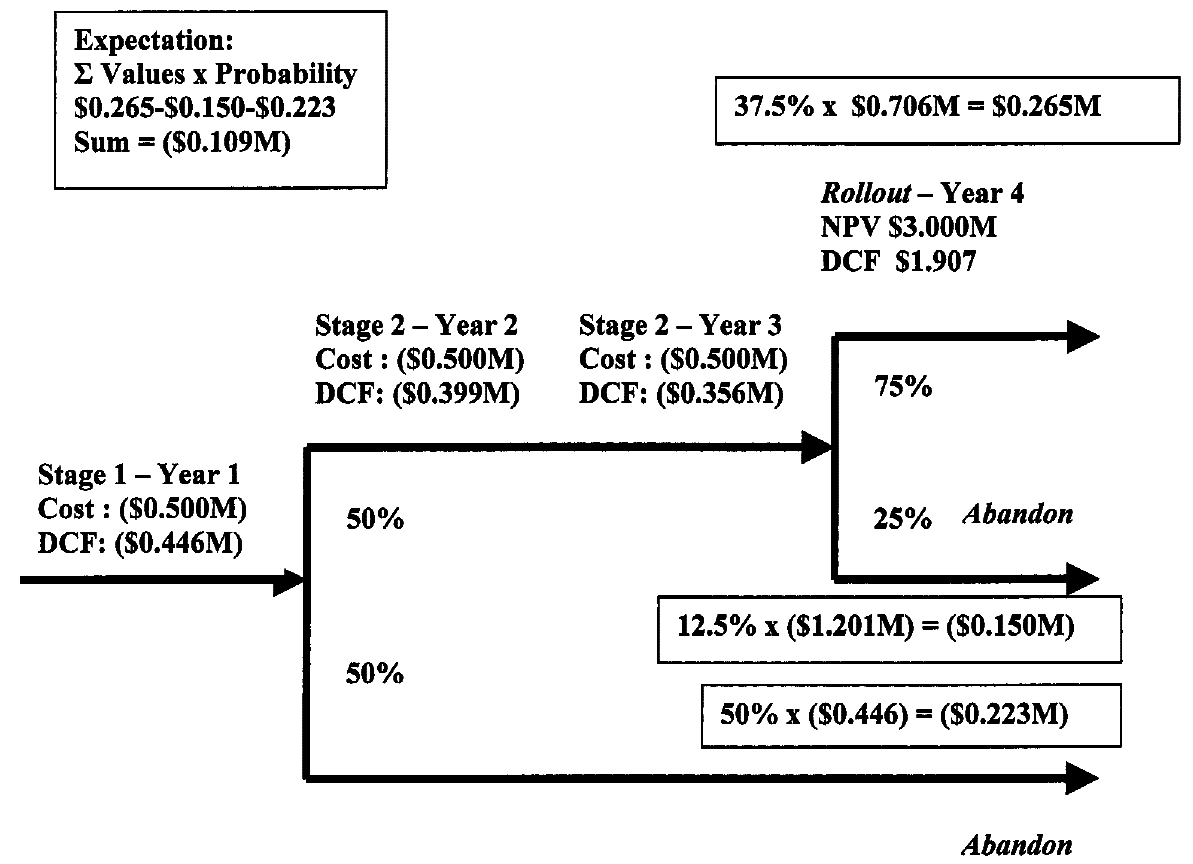
The project has abandonment scenarios after Stages 1 and 2, and one successful outcome with a 37.5% chance of success. The expectation value on the upper left is the weighted sum of the three possible outcomes. (M = million.) (Boer, 2003, p. 54)

Project Outcome by Real Options Analysis

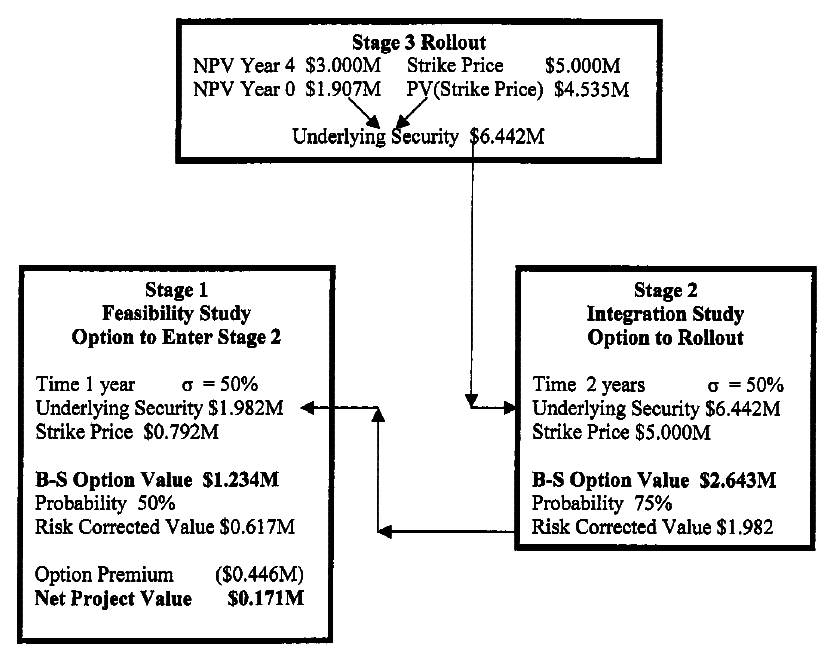
The Real Options calculation begins with value of a successful Rollout (top). This value is the underlying security for the Integration Study Option (lower right), which is in turn the underlying security for the Feasibility Study (lower left).  (Boer, 2003, p. 55)

Project Outcome by Real Options Analysis, assuming Zero Volatility

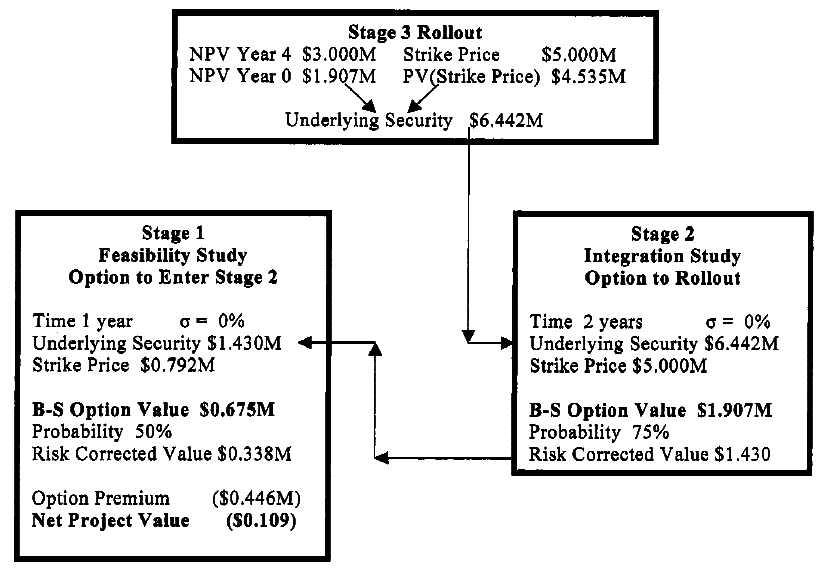
The dynamics are identical to Figure 2, with volatility set equal to zero. The result equals that of Figure 1. (Boer, 2003, p. 55)

Example of integrating NPV, Decision Trees and Real Options

This is another fictitious example, this time focused on developing a new polymer. A research group has estimated it would take eight years of R&D to get ready for commercial operations, and that sales would rise from an initial year’s \$12 million, to \$48 million five years after launch.

The top tier shows a sales forecast, capital requirements and cost data for a proposed business, along with financial parameters. The second tier shows the R&D project estimates: cost, time and duration for each R&D stage. At the bottom left is the calculated initial investment and the value of the business plan using five possible assumptions about terminal value. At the bottom right is the current value of the project and the value progression after each successful project stage.  (Boer, 2003, p. 56)

Terminal value represents the value of a business in a horizon year, which is a year that far enough that further cash flow calculations are not needed.

If the company wishes to liquidates the business in the horizon year, then terminal value is equal to the working capital and fixed assets.

If there is still viable business in the horizon year, Boer lists three ways to estimate the terminal value:

• as a multiple of income (using Price-to-Earnings ratio),
• as a multiple of pre-tax Cash Flow (EBITDA), or
• as a function of Free Cash Flow using the growth-in-perpetuity method.

Usability of the unified approach to valuation of R&D projects

Boer believes that this unified approach to valuation is also useful for evaluating startup companies, drawing the parallel between financing rounds and R&D stages.

He also argues that once we have determined the base case we can run sensitivity analysis or Monte Carlo simulation on any parameter in order to determine the full range of uncertainty.

When does adding Real Options to the economic analysis make a difference

Boer argues that Real Options contribute the most when it comes to tough and difficult decisions. He warns that achieving turbocharged valuations via Real Options will not be a universal result, despite the fact that market risk always acts in the direction of enhancing value.  (Boer, 2003, p. 57)

Options that are either deep-in-the-money or deep-out-of-the-money do not benefit from Real Options. On the other hand, options that are at-the-money or slightly-out-of-the-money have most to gain from the Decision Tree/Real Options approach.  (Boer, 2003, p. 57)

(At-the-money and slightly-out-of-the-money refers to zero or slightly negative Net Present Value.)

References

Boer, F. P. (2003). Risk-Adjusted Valuation of R&D Projects. Research-Technology Management, 46(5), 50–58.