Reading notes: A real-world way to manage real options
An argument for binomial (lattice) models and boring decisions.

Table of Contents
A common critique of real options approach is that management decision options are more complex and ambiguous than financial options, and that assumptions in the Black-Scholes-Merton model make it less than ideal choice for valuing real options.
Copeland and Tufano (2004, p. 2) argue that:
- binomial model is more appropriate because it captures the contingencies of real options and addresses nearly all of the most commonly voiced criticisms of using option theory to manage those contingencies, and
- the biggest problem with real options is failing to exercise them optimally, i.e. exercising them too early or too late.
Choosing the right model
Two main differences between financial and real options are:
- it's easier to gather information required to value financial options, than it is for real options, and
- the right to exercise financial options is unambiguous.
Both financial and real options require assumptions for them to work, hence they are not different in that regard.
Copeland and Tufano (2004, p. 3) explain that Black-Scholes-Merton model was designed to value an option that was exercisable only at the end of its life and whose underlying share paid no dividends, and that it was never intended for use with more complicated derivatives, such as compound options, and attempts to use it for real-option valuation are misguided and inappropriate.
Authors argue that binomial (lattice) models is more suited for valuing real options because they use algebra, meaning:
- they can be built using standard spreadsheet software,
- mathematics is simpler, but there is more of it, and
- it's easier to understand and tweak.
They argue that all the extra work isn't a problem because managers need to build spreadsheets for NPV analysis anyway. On ease of understanding and tuning, they write that instead of having to make guesses about the “volatility” of a project’s returns, for example, managers can think about the probability that a company’s revenues will rise or fall by a particular percentage. (Copeland & Tufano, 2004, pp. 3–4)
The binomial model in action
Authors demonstrate the model on the example of Copano, a fictional commodity chemical company considering an investment in a new plant.
Modeling the value of the underlying asset
Authors begin by estimating the present day value of the asset using the discounted cash flow technique. Then they estimate how much is the value going to go up or down in the analysed time period. Assuming that values are distributed fairly standard or lognormal, the factor for moving up is $\sigma \sqrt{t}$, while the factor for moving down is $1/e^{\sigma \sqrt{t}}$. Volatility, $\sigma$, can be estimated by looking at the key value drivers and how they influence the asset value.
Using that approach they construct Copano's event tree:
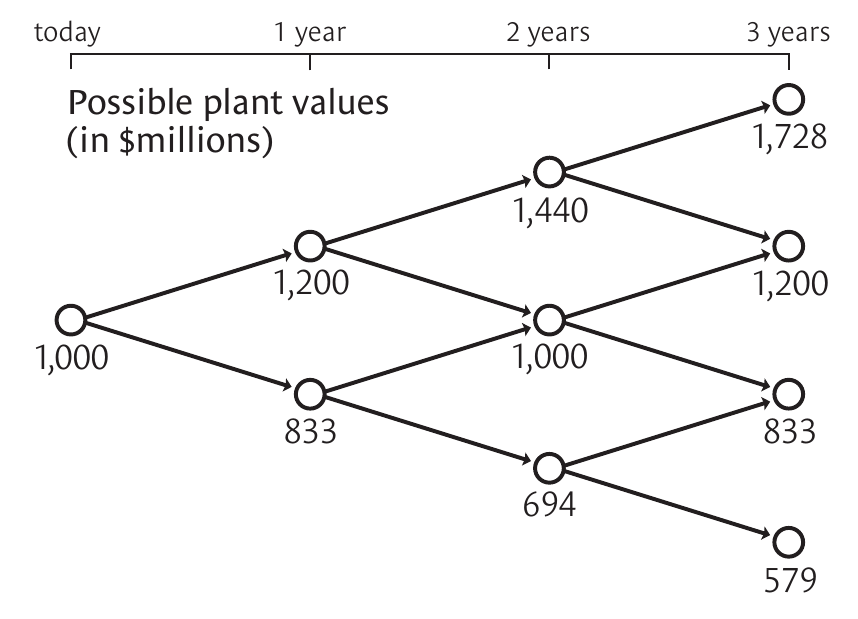
Valuing your options
Each node in the decision tree represents an option. Authors work backwards, starting from year 3. Option value is calculated by subtracting investment / exercise cost from the asset value. For other years they compare two values: exercising the option immediately and keep the option open. Replicating portfolio technique is used to calculate the value of keeping an option open.
After completing all the calculations, we get to Copano's decision tree:
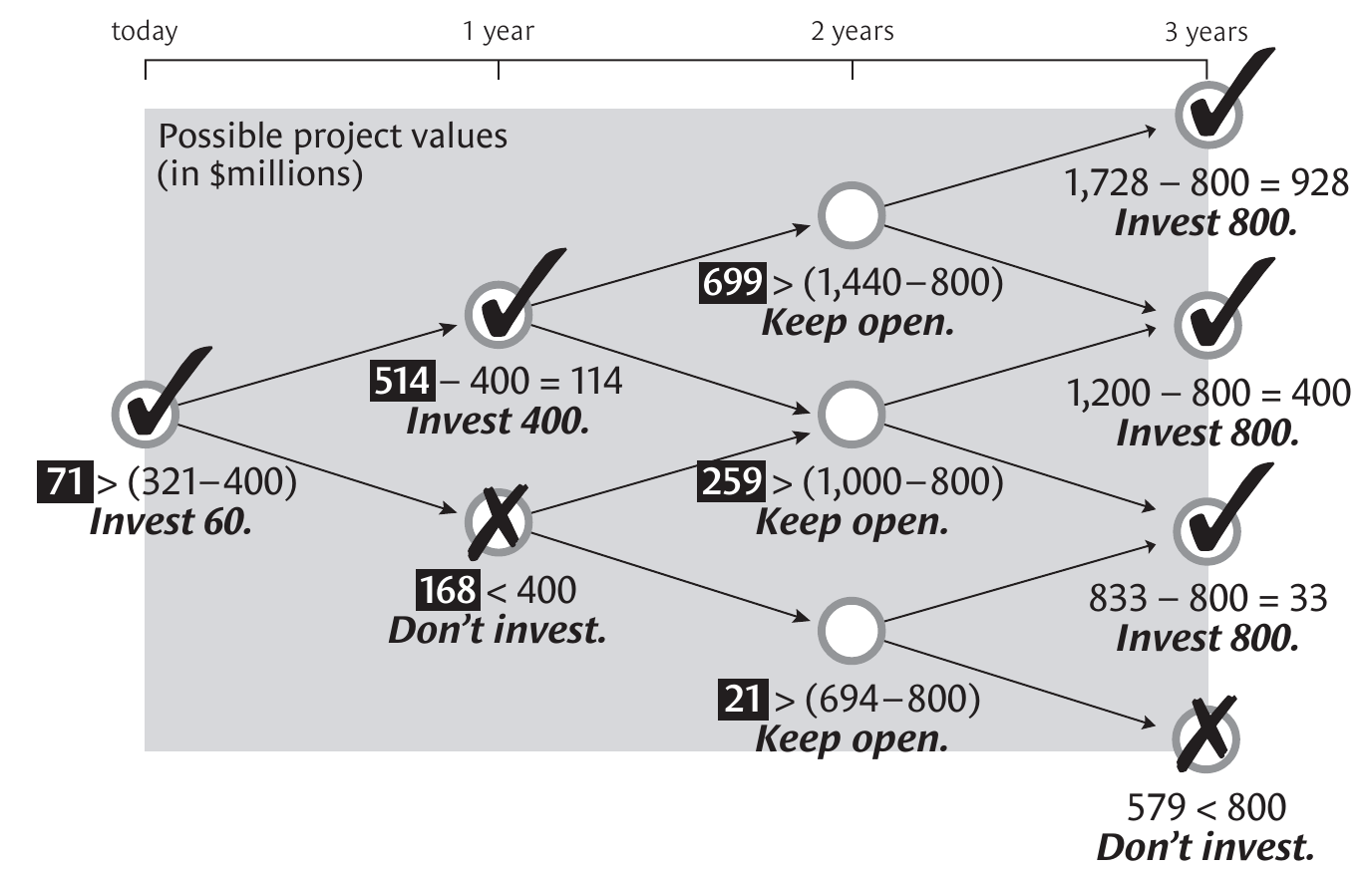
Copeland and Tufano (2004, p. 7) suggest that savvy managers should be thinking not only about today’s value but also the range of future outcomes.
The problem of poor exercise
Copeland and Tufano (2004, p. 7) argue that the real reason that real options sometimes turn out to be less valuable than predicted by models is that managers don’t exercise their option rights in a timely and rational manner.
Exercising – as in, deciding to invest – too early or too late destroys value. Authors share two examples, one where exercising too late can destroy up to 68% of the value, and one where exercising too early can destroy up to 91% of the value:
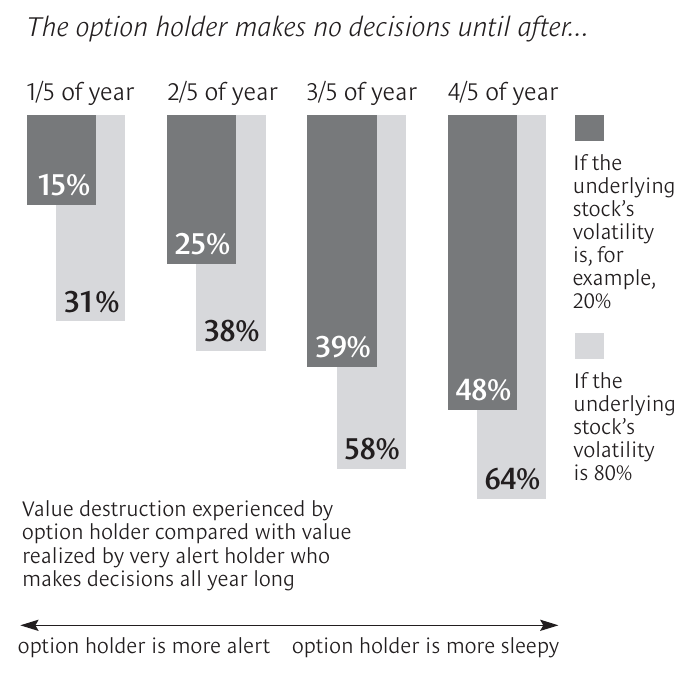
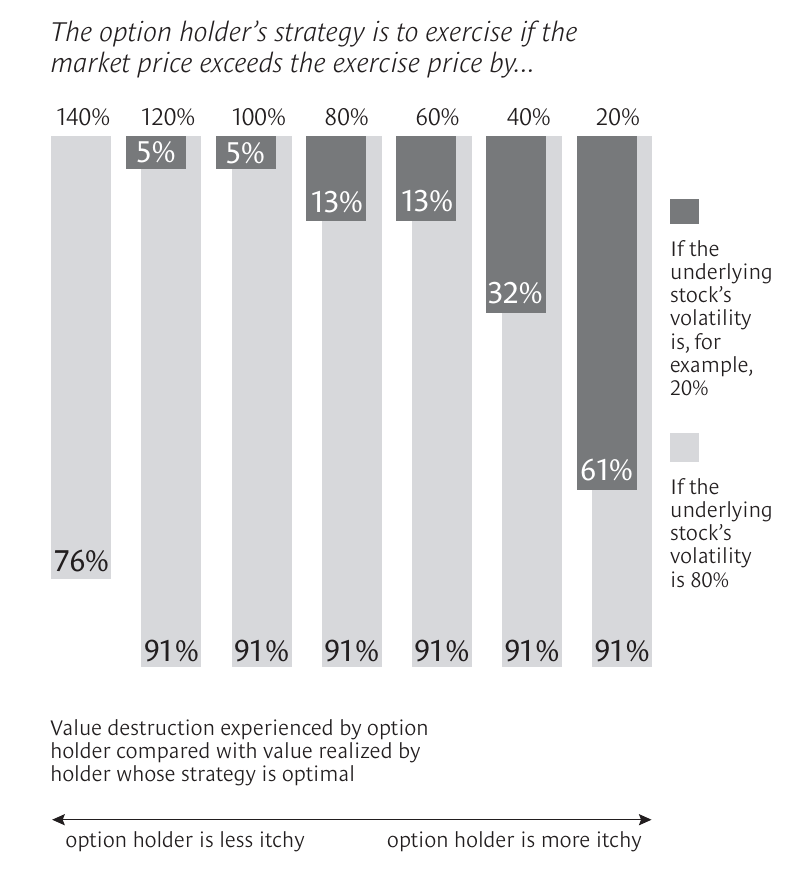
Managing binomially
In order to help managers improve how they exercise options, authors propose that organisation should define decision trigger points that correspond to the nodes on a binomial decision tree. (Copeland & Tufano, 2004, p. 9)
Trigger points should be defined as ranges, and have a clearly designated person who is making a decision to exercise or not. Authors compare it to a warning light to be ignored only if the pilot really knows better.
Their argument how some of the best decisions are to shut down unprofitable operations or wait for conditions to improve strongly resonates with me:
Although the decision to exercise an option can be visible and exciting (ground-breaking ceremonies, banners, press releases), some of the best option-exercise decisions aren’t flashy. They are decisions like shutting down unprofitable operations or waiting until conditions improve. They can create massive amounts of value, but they don’t lend themselves to stories in the company newsletter. Companies need to find ways to reward the people who make these decisions, using means such as combinations of compensation, increased responsibility, and public acknowledgement. (Copeland & Tufano, 2004, p. 10)
References
Copeland, T. E., & Tufano, P. (2004). A real-world way to manage real options. Harvard Business Review, 82(3), 90–99.
Bruno Unfiltered
Subscribe to get the latest posts delivered right to your inbox. No spam. Only Bruno.




