Reading notes: Investment opportunities as real options
On viewing strategic decisions as options.

Table of Contents
Luehrman promises to give us a way to apply option pricing to strategic decisions without hiring an army of Ph.D.’s. How did that go?
In this HBR piece, Luehrman proposes a framework for applying real options to valuation of investment opportunities–without needing to hire an army of PhD's. His approach depends on organisation already using discounted cash flow analyses (DCF) when estimating net present value (NPV).
Mapping a project onto an option
Luehrman argues that a corporate investment opportunity is like a call option because the corporation has the right, but not the obligation, to acquire something. (Luehrman, 1998, p. 3) By pricing an investment opportunity like an option we can learn more about its value than if we were just to use discounted cash flow analysis. He uses the structure of a call option to map an investment opportunity:
| Variable | Call option | Investment opportunity |
|---|---|---|
| $S$ | Stock price | Present value of a project’s operating assets to be acquired |
| $X$ | Exercise price | Expenditure required to acquire the project assets |
| $t$ | Time to expiration | Length of time the decision may be deferred |
| $r_f$ | Risk-free rate of return | Time value of money |
| $σ^2$ | Variance of returns on stock | Riskiness of the project assets |
Linking NPV and option value
When the time to decide on investment has run out NPV and option value are identical. Mathematically, when t equals zero, option value is the greater of $S-X$ or zero. In other words, if you are already calculating NPV for your investments you should be able to easily calculate $S$ and $X$ without introducing new models.
Luehrman argues that deferring investment decision is valuable because we can (1) earn the time value of money on the deferred expenditure, and (2) the value of the operating asset we intend to acquire might change. (Luehrman, 1998, p. 5)
Quantifying extra value with $NPVq$
NPVq is the interest we can earn on the required capital expenditure by investing later rather than sooner. It is calculated as quotient between cost $S$ and present value $PV(X)$: $NPVq=\frac{S}{PV(X)}$
Quantifying extra value with cumulative volatility
While we are waiting to decide an assets value may change, which may lead us to making a better decision. Luehrman quantifies the value of this by introducing cumulative volatility, derived from cumulative variance. Variance per period is used as a measure of uncertainty in the future valuation of the asset
Cumulative variance is expressed as variance per period times the number of periods: $\sigma^2 t$. Luehrman refines it by stating that we will use variance of project returns instead of project values, and that we will use standard deviation instead of variance. Benefit of the latter is that standard deviation is in the same unit as the thing we are measuring.
By implementing his refinements, we come to cumulative volatility, $\sigma \sqrt{t}$.
Luehrman (1998, p. 10) proposes three ways to estimate cumulative volatility:
- Take an educated guess. Assets with higher risk are more likely to also have higher $σ$ values.
- Gather some data. We can use (1) historical data on investment returns in the same or related industries, or (2) current prices of options traded on organized exchanges to calculate implied volatility.
- Simulate $σ$. Use Monte Carlo simulation to generate probability distribution for project returns, then compute its standard deviation.
Valuing the option with Luehrman's call-option metrics
Luehrman's $NPVq$ and $\sigma \sqrt{t}$ contain all the Black-Scholes variables required to value the investment opportunity as a European call option:
| Investment opportunity | Call option | Variable | $NPVq$ | $\sigma \sqrt{t}$ |
|---|---|---|---|---|
| Present value of a project’s operating assets to be acquired | Stock price | $S$ | ✓ | |
| Expenditure required to acquire the project assets | Exercise price | $X$ | ✓ | |
| Length of time the decision may be deferred | Time to expiration | $t$ | ✓ | ✓ |
| Time value of money | Risk-free rate of return | $r_f$ | ✓ | |
| Riskiness of the project assets | Variance of returns on stock | $σ^2$ | ✓ |
Higher $NPVq$ and $\sigma \sqrt{t}$ mean higher valuation, as demonstrated in the example:
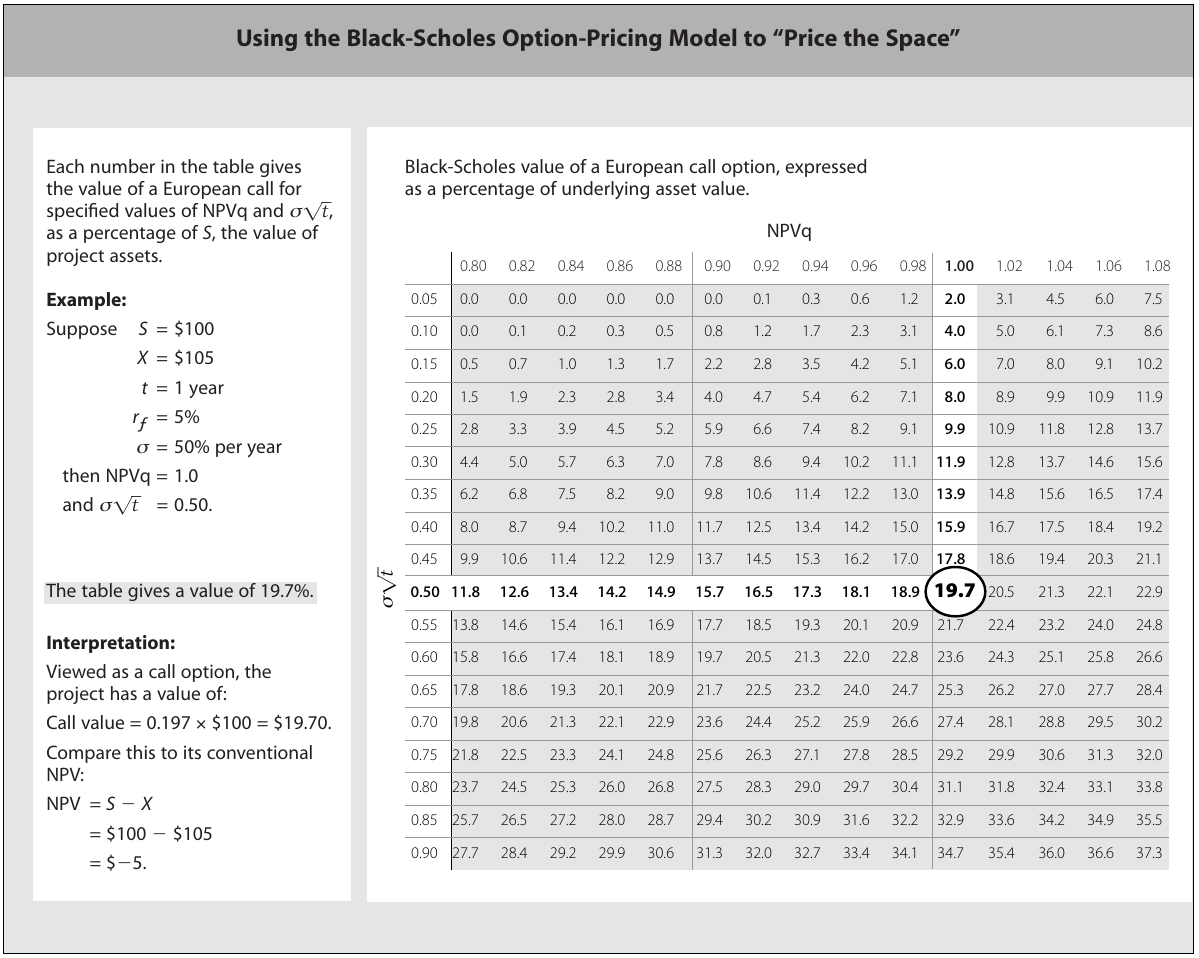
Luehrman's framework in seven steps
Luehrman's (1998, pp. 9–13) explains his example by breaking it in seven steps:
- Recognize the option and describe it.
- Map the project’s characteristics onto call option variables.
- Rearrange the DCF projections to separate phases and isolate values for $S$ and $X$.
- Establish a benchmark for phase 2’s option value based on the rearranged DCF analysis.
- Attach values to the option-pricing variables.
- Combine the five option-pricing variables into the option-value metrics, $NPVq$ and $\sigma \sqrt{t}$.
- Look up call value as a percentage of asset value in the Black-Scholes option-pricing table.
Luehrman on extending his framework
Luehrman (1998, p. 14) discusses following limitations of his framework:
- it assumes that the amount and timing of a project’s capital expenditures ($X$) are certain;
- many real options are American rather than European, i.e. they can be exercised at any time; and
- if the Black-Scholes assumptions fail to hold, the framework yields qualitative insights but the numbers become less reliable.
References
Luehrman, T. A. (1998). Investment opportunities as real options: Getting started on the numbers. Harvard Business Review, 76(4), 51–67.
Bruno Unfiltered
Subscribe to get the latest posts delivered right to your inbox. No spam. Only Bruno.




